This activity reveals the odds of winning the Lottery and of other events. It gives the opportunity to discuss the differences between the perception and the reality of winning the National Lottery.

4.

Provide feedback by giving the
correct odds for each event, so that
the young people can rearrange
their cards in the correct order (as
you do so, you could hand them out
the ‘odds cards’ to be matched to
each event, as a visual aid).

Alternative options:

If it’s a big group, you could divide it into teams and
use multiple sets of cards.

You could give 1 card to each person and then ask the
group to stand up, forming a line from the person with
the most likely event to the one with the least likely
event. Then proceed from step 3.

What are the odds?

5. Encourage discussion of the correct likelihood for each event and how perception might affect one’s choices of gambling. Particularly, reflect on the implications of 1:97 chances of winning £30 with a lottery ticket (minimum cash win at the national lottery, when matching 3 main numbers):

• this is of course much more likely than winning the jackpot (1:45 million);

• 1:97 means that on an average every 97 tickets there is one winning ticket for £30 (yet it’s an average, so sometimes there could be none and in other cases there could be more than one £30 winning ticket);

• given that 1 lottery ticket costs £2, even if I win £30 once, the reality is that every 97 tickets I will have spent £194 to get £30 back, so I will be still in a loss of £164;

• on average, for every 97 people who buy 1 lottery ticket each, there will be just 1 person winning £30, yet this winner will usually tell other people about the £30 win, whilst all those who have lost will stay quiet. This may change people’s perceptions, who might not realise how common losing is.

What are the odds?

Events Handout Cards

What are the odds?

Odds Handout Cards

What are the odds?

Practitioner Answer Sheet

What are the odds?

Practitioner Notes: Recent Changes to the National Lottery

Since October 2015, players can pick 6 numbers from a total of 59 numbers, instead of the 49 numbers played in the old National Lottery. Adding 10 numbers has made winning a cash prize less likely than before:

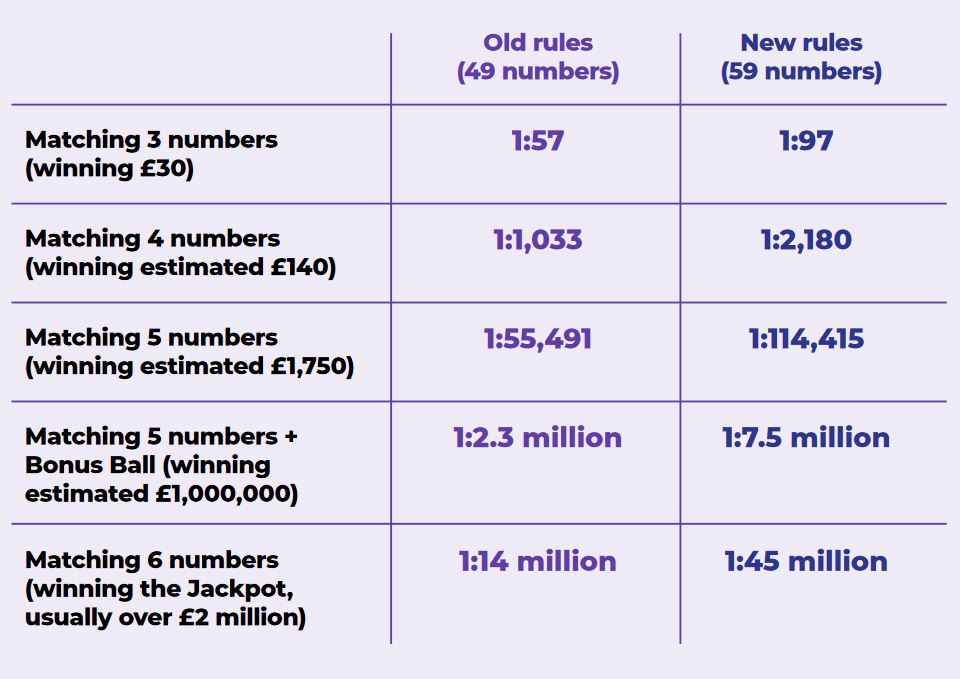
To compensate this change, a new prize has been added. Now, when matching two numbers, the player wins a “Free Lotto Lucky Dip”, meaning a new lottery ticket – it’s not possible to take the money instead.

A National Lottery Ticket costs £2.

The odds of winning any prize playing EuroMillions are one in 13. The odds of winning the EuroMillions jackpot is much higher, at 1 in 139,838,160.